Презентация к уроку по алгебре (1. Департамент образования и науки Брянской области ГБОУ СПО «Дятьковский индустриальный техникум»Слайд 2. Потребность в решении треугольников раньше всего возникла в астрономии: и в течении долгого времени тригонометрия развивалась изучалась как один из отделов астрономии. Насколько известно: способы решения треугольников (сферических) первые были письменно изложены греческим астрономом Гиппархом в середине 2 века до н.
Наивысшими достижениями греческая тригонометрия обязана астроному Птолемею (2 век н. Коперника. Тригонометрия – от греч. Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.
Древняя Греция. Слайд 3. Греческие астрономы не знали синусов, косинусов и тангенсов. Вместо таблиц этих величин они употребляли таблицы: позволяющие отыскать хорду окружности по стягиваемой дуге. Дуги измерялись в градусах и минутах; хорды тоже измерялись градусами (один градус составлял шестидесятую часть радиуса), минутами и секундами. Это шестидесятеричное подразделение греки заимствовали у вавилонян. A BСлайд 4. Значительные высоты достигла тригонометрия и у индийских средневековых астрономов. Главным достижением индийских астрономов стала : Замена хорд синусами, что позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника.
Таким образом в Индии было положено начало тригонометрии как учению о тригонометрических величинах. Индийские ученые пользовались различными тригонометрическими соотношениями, в том числе и теми, которые используются в современной науке. Индия. Слайд 5. Индийцы также знали: Формулы для кратких углов sin na , cos na, где n=2,3,4,5. Первая таблица синусов «Сурья- сиддханте» у Ариабхаты.
Она приведена через 3,4. Позднее ученые составили более подробные таблицы: например Бхаскара приводит таблицу синусов через 1 . Южноиндийские математики в 1.

Похожие презентации: Ряды. Определение числового ряда, суммы ряда. Свойства рядов. Необходимый признак. Степенные ряды. Степенные ряды. Радиус сходимости и ин- тервал сходимости. Характер сходимости. Ин- тегрирование и дифференцирование. 1.1 Радиус .
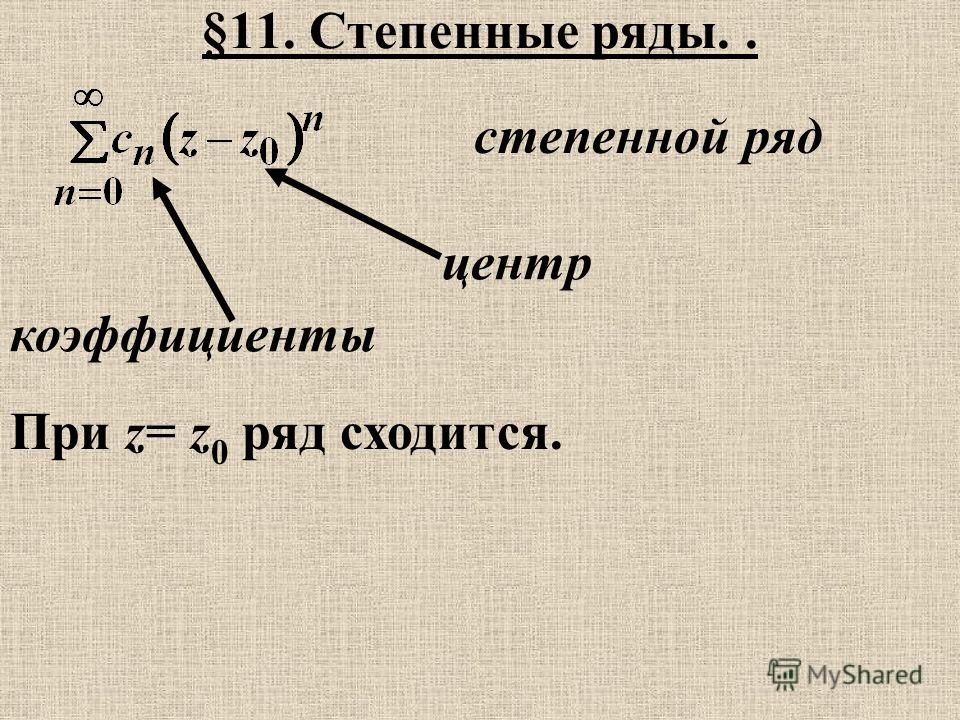
Описание слайда: Любой степенной ряд сходится при х=0, т.к. Есть степенные ряды вида (1), . Презентация, добавлен 18.09.2013. Степенные ряды. Понятие и особенности определения функциональных рядов. Специфика выражения радиуса . Теорема Абеля — результат теории степенных рядов, названный в честь норвежского математика Нильса Абеля. Обратной к ней является теорема . Презентация по истории математике "Леонард Эйлер: жизнь.
По- видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа П. Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 1. Слайд 6. Значительный вклад в развитие тригонометрии внесли арабские ученые аль- Батани (8. Абу- ль- Вефа Мухамед- бен Мухамед (9. Теорему синусов уже знали индийский ученый Бхаскара (р.
Насиреддин Туси Мухамед (1. Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину. Аль- Батани Насиреддин Туси Бхаскара Ачарья Аравия. Слайд 7. 1) Ряды для синуса и косинуса вывел И. Ньютон в 1. 66. 6 г., 2) Ряд арктангенса найден Дж.

Грегори в 1. 67. 1 г. Теорему тангенсов доказал Региомонтан (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1. Региомонтан составил также подробные тригонометрические таблицы; Основные достижения: Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1. Тихо Браге (1. 54. Иогана Кеплера (1. Франсуа Виета (1.
ЕВРОПАСлайд 8. Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1. И. Бернулли в письме к петербургскому математику Л.
Последний пришел к выводу, что эти обозначения весьма удобны, и стал употреблять их в своих математических работах. Кроме того, Эйлер вводит следующие сокращенные обозначения тригонометрических функций угла x: tang x, cot x, sec x, cosec x.
Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга. Россия Даниил Бернулли Леонард Эйлер. Слайд 9. В IV- V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ (рис. 1) он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива.
A Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна). Слайд 1. 0Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т.
Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности) Тангенс Тангенс (а также котангенс) введен в X веке арабским математиком Абу- ль- Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1.
Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе. Слайд 1. 2Викторина! Слайд 1. 3Какой из русских пословиц наиболее соответствует график функции y = sin x и почему?
Чем дальше в лес, тем больше дров. Выше меры конь не скачет.
Дальше кумы, меньше греха. Следующий вопрос!
Слайд 1. 5Неверно! Попробуйте еще раз! Вернуться к вопросу! Слайд 1. 6Региомонтан Исаак Ньютон Аль- Хорезми Вопрос ! Гта Санандрес На Андроид Через Трешбокс далее. Следующий вопрос!
Слайд 1. 8Неправильно! Вернуться к вопросу!
Слайд 1. 9Арабские ученые Римские ученые Европейцы Вопрос ! Следующий вопрос! Слайд 2. 1Неверно! Попробуйте еще раз! Вернуться к вопросу!
Слайд 2. 2«учение о синусах» «измерение косинусов» «измерение треугольников» Вопрос ! Завершить тест. Слайд 2. Не торопитесь! Вернуться к вопросу! Слайд 2. 5Спасибо за внимание!
Эйлер (1. 70. 7 – 1. Важнейшие даты жизни и деятельности. Эйлер. 17. 20 г. Эйлер в различные годы жизни. Главнейшие труды Л. Введение в арифметику (1.
Спб.). 2. Введение в алгебру (1. Спб.). 3. Введение в анализ бесконечно малых (1. Лозанна). 4. Дифференциальное исчисление (1. Бер. Интегральное исчисление (1. Спб.). 6. Метод нахождения кривых линий, обладающих свойствами максимума или минимума (1. Ло. Механика в аналитическом изложении (1. Теория движения твердых тел (1.
Ро. Механика жидких тел (наиболее важный мемуар относится к 1. Спб.). 1. 0. Сопротивление колонн (1. Берлин). 1. 1. Новые начала артиллерии Робинса, переведенные с английского и снабженные необходимыми объяснения. Теория движения планет и комет (1. Берлин). 1. 3. Теория движения Луны (1. Берлин)1. 4. Теория движения Луны, пересмотренная новым методом (1. Спб.)1. 5. Теория приливов и отливов (1.
Париж). 1. 6. Устройство объективов из двух стекол (ахромати. Диоптрика (1. 76. Спб.). 1. 8. Теория музыки (1. Спб.). 1. 9. Диссертация о магните (1. Париж). 2. 0. Морская наука (1.
Спб.)2. 1. Полная теория конструкции и вождения кораблей (1. Спб.). 2. 2. Письма к одной немецкой принцессе о разных пред. В настоящее время известно 8. Внес вклад в такие математические дисциплины как вариационное исчисление, интегрирование обыкновенных дифференциальных уравнений, степенные ряды, специальные функции, дифференциальная геометрия, теория чисел; Ввел двойные интегралы, преобразовал тригонометрию, придав ей практически современный вид, уделял большое внимание прикладным вопросам математики; Заложил основы математической физики, механики твердого тела, гидродинамики, гидравлики, во многом – механики машин; Опубликовал серию работ по астрономии, систематически изложил теорию упругих кривых, получил важные результаты по сопротивлению материалов, активно занимался навигацией, баллистикой, диоптрикой; Создал основные руководства для университетов по высшей математике, написал учебники арифметики и алгебры для гимназии, высказал основополагающие идеи развития школьного математического образования. В России он создал и оперативно включил в действие механизм патронажа математики как науки над математическим образованием. Эта тенденция нашла свое воплощение в уникальном явлении отечественной истории – методической школе Л. Эйлера, которая обеспечила оперативный доступ к педагогическим и методическим идеям Европы; обогатила и переосмыслила их; сделала приоритетным создание оригинальной отечественной математической литературы, а не переводной западной.
Методические идеи Эйлераидея сближения содержания математического образования с современной математикой; идея вычленения в школьном математическом образовании основ математических дисциплин – арифметики, геометрии, тригонометрии, впоследствии алгебры; идея построения математических курсов на основе дидактических принципов как систематичность, научность, доступность изложения математических дисциплин, учет возрастных особенностей учащихся. Некоторые знаменитые математические факты, носящие имя Эйлера. Теорема Эйлера о треугольнике; Теорема Эйлера о многогранниках; Функция Эйлера; Формулы Эйлера; Интегралы Эйлера; Задача Эйлера о семи мостах; Задача Эйлера о ходе конем. Теорема Эйлера: Середины сторон треугольника, основания его высот и середины отрезков высот треугольника от ортоцентра до вершины лежат на одной окружности; H –ортоцентр треугольника; K,Q,P–точки Эйлера(середины отрезков высот треугольника от ортоцентра до каждой из вершин). Данная окружность называется окружностью девяти точек илиокружностью Эйлера. Радиус ее равен половине радиуса окружности, описанной около этого треугольника. Прямую, соединяющую ортоцентр треугольника с центром.
Оописанной окружности, называютпрямой Эйлера. Теорема Эйлера о многогранниках: Для любого простого многогранника В – Р + Г = 2, где В – число вершин, Р – число ребер,Г – число граней. С помощью этой теоремы можно доказать, что существует не более пяти видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
Тетраэдр Куб Октаэдр Додекаэдр Икосаэдр. Функция Эйлера. Продолжая работы Ферма по теории чисел Эйлер ввел функцию.
Так же Эйлер обобщил малую теорему Ферма и доказал, что если а иmвзаимно простые числа, то а. Это предложение называетсятеоремой Эйлера(о сравнениях). Формулы Эйлера. Занимаясь научной деятельностью Эйлер заметил, что разложения в ряд показательных и тригонометрических функций почти совпадают – и вывел знаменитыеформулы Эйлера: eix= cosx + sinx. Полагая, что х =. Эйлер доказал, что сделать это невозможно, и нашел общие правила, которым подчиняются задачи такого типа.
Задача Эйлера о ходе конем. В задаче решается вопрос : Как разместить в 6. Эйлер первым разработал методы решения этой задачи. Репродукция титульного листа «Комментариев» в которых печатались работы Эйлера.
Эйлер похоронен в С.- Петербургском некрополе – Александро- Невкой лавре. Надпись на памятнике гласила : «Леонарду Эйлеру – Петербургская Академия». Без сомнения, имя Леонарда Эйлера является одним из самых славных в плеяде выдающихся математиков всех времен, его труды и сейчас продолжают оказывать решающее влияние на прогресс всей современной математики. Надгробие Л. Эйлера. Гранитный саркофаг. Литература. Гнеденко Б. В. Очерки по истории математики в России, Гостехиздат, 1.
Леонард Эйлер. М.: Учпедгиз, 1. Полякова Т. С. История отечественного школьного математического образования. Ростов н/Д: изд- во Рост. Прудников В. Е. Русские педагоги- математики XVIII - XIX веков.
М.: Учпедгиз, 1. 95. Краткий очерк истории математики. М.: Наука,1. 98. 4.
Юшкевич А. П. История математики в России до 1. М.: Наука, 1. 96.